Note
Go to the end to download the full example code.
Generic Example#
This example shows how to use calculate the upwelling brigthness temperature by using R16 and R03 absorption model and then plotting them difference.
import matplotlib.pyplot as plt
plt.rcParams.update({'font.size': 15})
import matplotlib.ticker as ticker
from matplotlib.ticker import ScalarFormatter
import numpy as np
Import pyrtlib package#
from pyrtlib.climatology import AtmosphericProfiles as atmp
from pyrtlib.tb_spectrum import TbCloudRTE
from pyrtlib.utils import ppmv2gkg, mr2rh
atm = ['Tropical',
'Midlatitude Summer',
'Midlatitude Winter',
'Subarctic Summer',
'Subarctic Winter',
'U.S. Standard']
Load standard atmosphere (low res at lower levels, only 1 level within 1 km) and define which absorption model will be used.#
Performing upwelling brightness temperature calculation#
Default calculatoin consideres no cloud
Setup matplotlib plot
fig, ax = plt.subplots(1, 1, figsize=(12,8))
ax.set_xlabel('Frequency [GHz]')
ax.set_ylabel('${T_B}$ [K]')
rte = TbCloudRTE(z, p, t, rh, frq, ang)
rte.init_absmdl(mdl)
df = rte.execute()
df = df.set_index(frq)
df.tbtotal.plot(ax=ax, linewidth=1, label='{} - {}'.format(atm[atmp.TROPICAL], mdl))
ax.legend()
plt.show()
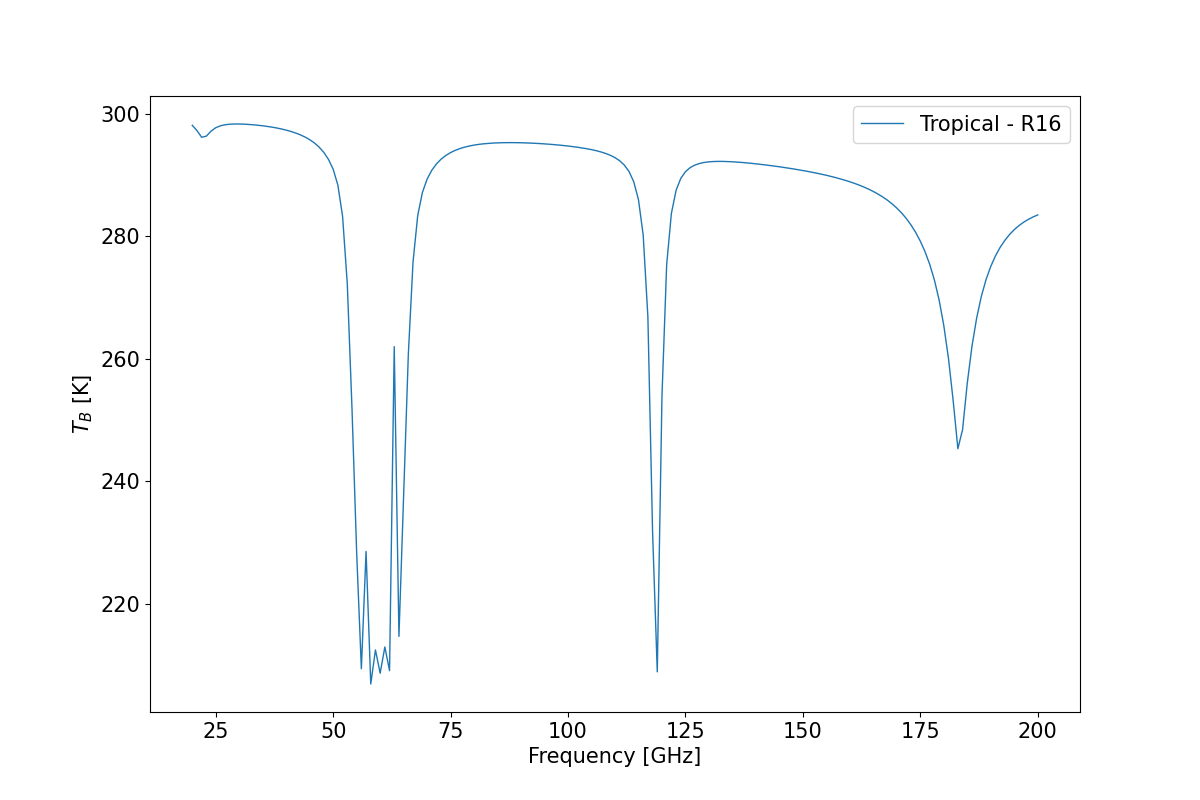
Print dataframe
Performing calculation for R03 absorption model#
Add brigthness temperature values as new column
df['delta'] = df.tbtotal - df_r03.tbtotal
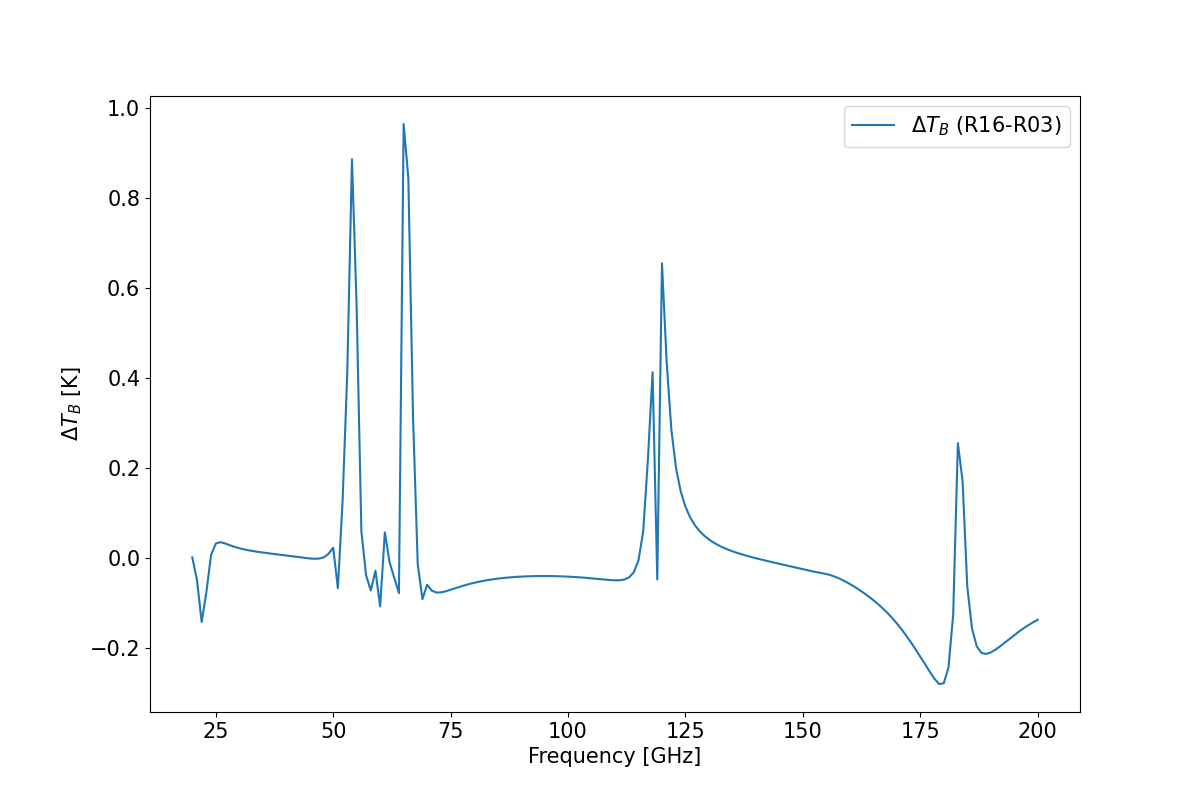
Difference between R16 and R03 brightness temperature
fig, ax = plt.subplots(1, 1, figsize=(12,8))
ax.set_xlabel('Frequency [GHz]')
ax.set_ylabel('$\Delta {T_B}$ [K]')
df.delta.plot(ax=ax, figsize=(12,8), label='$\Delta {T_B}$ (R16-R03)')
ax.legend()
plt.show()
/home/runner/work/pyrtlib/pyrtlib/docs/script_examples/generic_tutorial.py:108: SyntaxWarning: invalid escape sequence '\D'
ax.set_ylabel('$\Delta {T_B}$ [K]')
/home/runner/work/pyrtlib/pyrtlib/docs/script_examples/generic_tutorial.py:109: SyntaxWarning: invalid escape sequence '\D'
df.delta.plot(ax=ax, figsize=(12,8), label='$\Delta {T_B}$ (R16-R03)')
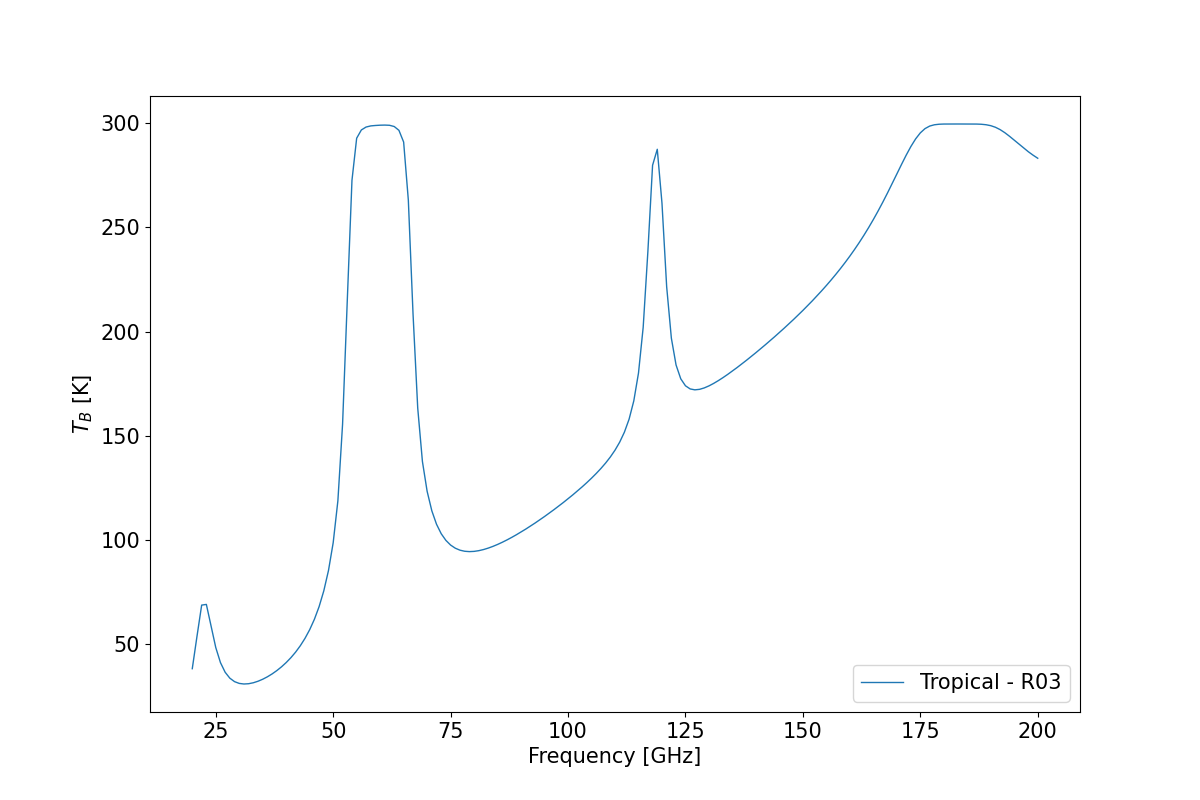
Performing downwelling brightness temperature calculation#
fig, ax = plt.subplots(1, 1, figsize=(12,8))
ax.set_xlabel('Frequency [GHz]')
ax.set_ylabel('${T_B}$ [K]')
rte.satellite = False
df_from_ground = rte.execute()
df_from_ground = df_from_ground.set_index(frq)
df_from_ground.tbtotal.plot(ax=ax, linewidth=1, label='{} - {}'.format(atm[atmp.TROPICAL], mdl))
ax.legend()
plt.show()
Total running time of the script: (0 minutes 14.609 seconds)
