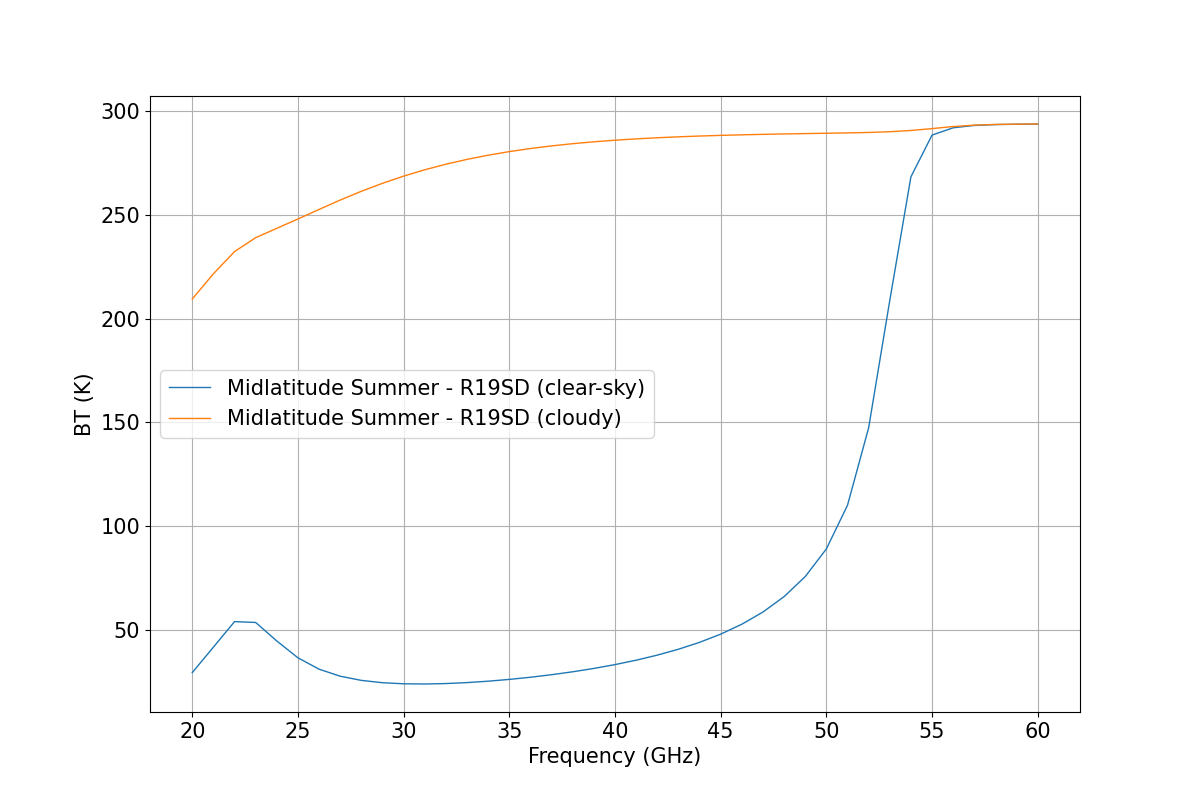
Performing Downwelling Brightness Temperature calculation in cloudy condition.

This example shows how to use the pyrtlib.tb_spectrum.TbCloudRTE method to calculate brightness temperature from ground (downwelling) in cloudy condition

import matplotlib.pyplot as plt
from matplotlib.ticker import FixedLocator, FormatStrFormatter
plt.rcParams.update({'font.size': 15})
import numpy as np
np.seterr('raise')

from pyrtlib.climatology import AtmosphericProfiles as atmp
from pyrtlib.tb_spectrum import TbCloudRTE
from pyrtlib.utils import ppmv2gkg, mr2rh

atm = ['Tropical',
       'Midlatitude Summer',
       'Midlatitude Winter',
       'Subarctic Summer',
       'Subarctic Winter',
       'U.S. Standard']

fig, ax = plt.subplots(1, 1, figsize=(12, 8))

z, p, d, t, md = atmp.gl_atm(atmp.MIDLATITUDE_SUMMER)
gkg = ppmv2gkg(md[:, atmp.H2O], atmp.H2O)
rh = mr2rh(p, t, gkg)[0] / 100

mdl = 'R19SD'

ang = np.array([90.])
frq = np.arange(20, 61, 1)
nf = len(frq)

denliq = np.zeros(z.shape)
denice = np.zeros(z.shape)
cldh = np.empty((2, 2))

for i in [False, True]:
    if not i:
        text_plot = 'clear-sky'
    else:
        # build a cloud
        ib = 1
        it = 3
        denliq[ib:it + 1] = 10 * np.ones((it - ib + 1))
        cldh[:, 0] = np.array([z[ib], z[it]])
        ib = 29
        it = 31
        denice[ib:it + 1] = 0.1 * np.ones((it - ib + 1))
        cldh[:, 1] = np.array([z[ib], z[it]])
        text_plot = 'cloudy'

    ax.set_xlabel('Frequency (GHz)')
    ax.set_ylabel('BT (K)')

    rte = TbCloudRTE(z, p, t, rh, frq, ang)
    rte.satellite = False
    rte.cloudy = i
    rte.init_cloudy(cldh, denice, denliq)
    rte.init_absmdl(mdl)
    df = rte.execute()

    df = df.set_index(frq)
    df.tbtotal.plot(x=frq, ax=ax, linewidth=1,
                    label='{} - {} ({})'.format(atm[atmp.MIDLATITUDE_SUMMER], mdl, text_plot))

ax.grid(True, 'both')
ax.legend()
plt.show()

/home/runner/work/pyrtlib/pyrtlib/pyrtlib/tb_spectrum.py:221: UserWarning: It seems that TbCloudRTE.cloudy attribute is not set to True. Sets it to True for running model in cloudy condition.
  warnings.warn("It seems that TbCloudRTE.cloudy attribute is not set to True. "