Uncertainty Example

This example shows how to use the uncertainty module by simulating the downwelling brightness temperature and then calculate the uncertainty due to uncertainties in ${O_2}$ and ${H_2 O}$ parameter.

import matplotlib.pyplot as plt

plt.rcParams.update({'font.size': 15})
import matplotlib.ticker as ticker
from matplotlib.ticker import ScalarFormatter
import numpy as np
import pandas as pd

Import pyrtlib package and tools

from pyrtlib.uncertainty import AbsModUncertainty, SpectroscopicParameter
from pyrtlib.climatology import AtmosphericProfiles as atmp
from pyrtlib.tb_spectrum import TbCloudRTE
from pyrtlib.absorption_model import O2AbsModel
from pyrtlib.utils import ppmv2gkg, mr2rh, get_frequencies, constants
from pyrtlib.uncertainty import covariance_matrix

Define spectroscopic parameters to be perturbed and them uncertainties

O2_parameters = {
    'O2S': range(1),
    'X05': [None],
    'WB300': [None],
    'O2gamma': range(34),
    'Y300': range(34),
    'O2_V': range(34)
}

HO2_parameters = {
    'con_Cf_factr': [None],
    'con_Cs_factr': [None],
    'gamma_a': range(1),
    'S': range(1),
    'con_Xf': [None],
    'SR': range(1),
    'con_Xs': [None]
}

parameters = {**SpectroscopicParameter.oxygen_parameters('R18'),
              **SpectroscopicParameter.water_parameters('R17')}

parameters['O2S'].uncer = parameters['O2S'].value / 100
parameters['X05'].uncer = 0.05
parameters['WB300'].uncer = 0.05
parameters['O2gamma'].uncer[0: 34] = np.array([0.05, 0.0138964, 0.0138964, 0.0138964, 0.0138964,
                                               0.0138964, 0.0138964, 0.0138964, 0.0138964, 0.0138964,
                                               0.0138964, 0.0138964, 0.0138964, 0.0138964, 0.0138964,
                                               0.0138964, 0.0138964, 0.0138964, 0.0138964, 0.0138964,
                                               0.0138964, 0.01131274, 0.01131274, 0.01453087, 0.01453087,
                                               0.01789881, 0.01789881, 0.02116733, 0.02134575, 0.02476584,
                                               0.02476584, 0.02839177, 0.02839177, 0.03203582])
parameters['Y300'].uncer[0: 34] = np.array([0.01, 0.00404133, 0.00502581, 0.00786035, 0.00820458,
                                            0.00935381, 0.00809901, 0.0078214, 0.00544132, 0.00460658,
                                            0.00225117, 0.00209907, 0.0039399, 0.00484963, 0.00799499,
                                            0.00878031, 0.01202685, 0.01261821, 0.01577055, 0.01615187,
                                            0.01907464, 0.01926978, 0.0218633, 0.02188287, 0.02416567,
                                            0.02401716, 0.02604178, 0.02575469, 0.02762271, 0.02720018,
                                            0.02897909, 0.02843003, 0.03019027, 0.02951218])
parameters['O2_V'].uncer[0: 34] = np.array([0.00288243, 0.04655306, 0.03914166, 0.06110402, 0.0494057,
                                            0.05728709, 0.06444876, 0.07279906, 0.06385863, 0.07007177,
                                            0.05963384, 0.06373721, 0.11789158, 0.12307213, 0.10151855,
                                            0.10427449, 0.08328802, 0.08486523, 0.10130857, 0.10244286,
                                            0.15750036, 0.15814743, 0.24421784, 0.24343211, 0.3084326,
                                            0.30576201, 0.34568212, 0.34107696, 0.36123446, 0.35507902,
                                            0.37305309, 0.36544166, 0.38490936, 0.37583782])

parameters['gamma_a'].uncer[0] = 0.039
parameters['S'].uncer[0] = 0.043 * 1e-25 * constants('light')[0] * 100
parameters['con_Xf'].uncer = 0.8
parameters['SR'].uncer[0] = 0.0014
parameters['con_Xs'].uncer = 0.6

SpectroscopicParameter.set_parameters(parameters)

Load standard atmosphere (low res at lower levels, only 1 level within 1 km) and define which absorption model will be used.

z, p, _, t, md = atmp.gl_atm(atmp.TROPICAL)

gkg = ppmv2gkg(md[:, atmp.H2O], atmp.H2O)
rh = mr2rh(p, t, gkg)[0] / 100

Use frequencies set of HATPRO Radiometer

interp = 0.5
frq = sorted(list(set().union(get_frequencies('hat'), np.arange(20, 60 + interp, interp).tolist())))

Performing uncertainty of brightness temperature

Default calculatoin consideres no cloud and no perturbation

rte = TbCloudRTE(z, p, t, rh, frq, amu=parameters)
rte.satellite = False
rte.init_absmdl('R17')
O2AbsModel.model = 'R18'
O2AbsModel.set_ll()
df = rte.execute()

df_out = pd.DataFrame()
df_out['freq'] = frq
df_out['tb'] = df.tbtotal

Calculate Jacobian matrix

\(Cov(T_{b}) = K_{p} \times Cov(p) \times K_{p}^T\)

cnt = 0
for k, v in (O2_parameters | HO2_parameters).items():
    for i in v:
        amu_p = AbsModUncertainty.parameters_perturbation([k], 'max', index=i)
        rte.set_amu(amu_p)
        df = rte.execute()
        if k =='O2S':
            parameters[k].uncer = parameters[k].uncer / parameters[k].value * 100
        if k in ['con_Cf_factr', 'con_Cs_factr']:
            parameters[k].uncer = parameters[k[0:6]].value * parameters[k].uncer
        field_name = 'p_{}{}'.format(k, '_' + str(i) if i else '')
        delta_tb = df.tbtotal.values - df_out.tb.values
        if i is not None:
            o = pd.Series(delta_tb / parameters[k].uncer[i], name=field_name)
        else:
            o = pd.Series(delta_tb / parameters[k].uncer, name=field_name)
        df_out = pd.concat([df_out, o], axis=1)
        cnt += 1

Calculate uncertainty (sigma) for BT

Using covariance matrix by [Cimini-2018] which identifies 111 parameters (6 for water vapor and 105 for oxygen)

params = df_out.copy()

Kp = df_out.loc[:, ~df_out.columns.isin(['tb', 'freq', 'p_con_Xs'])].values
covtb = np.matmul(np.matmul(Kp, covariance_matrix.R17_111), Kp.T)
sigma_tb = np.sqrt(np.diag(covtb))
params['sigma_tb'] = sigma_tb

Using covariance matrix by [Cimini-2019] which add the \({n_{CS}}\) parameter for water vapour

Kp = df_out.loc[:, ~df_out.columns.isin(['tb', 'freq'])].values
covtb = np.matmul(np.matmul(Kp, covariance_matrix.R17_112), Kp.T)
sigma_tb = np.sqrt(np.diag(covtb))
params['sigma_tb_with_con_Xs'] = sigma_tb

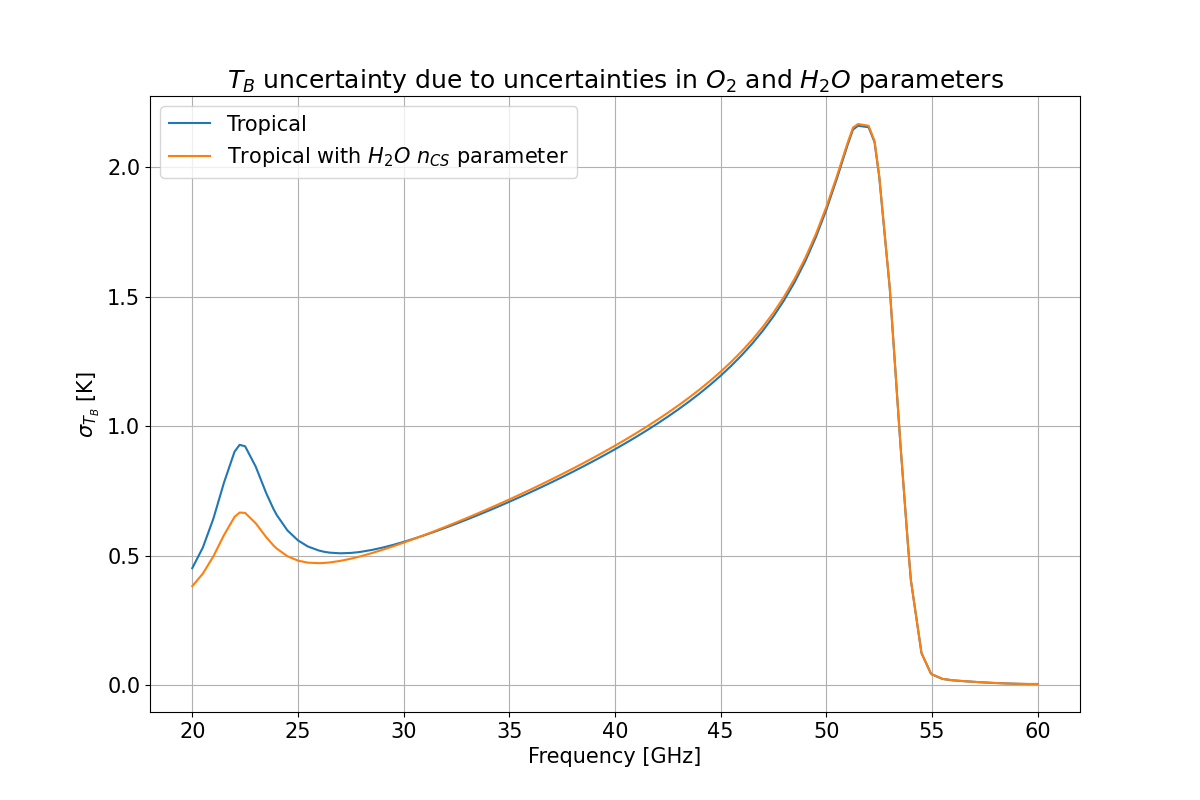
params.plot(x='freq', y=['sigma_tb', 'sigma_tb_with_con_Xs'],
            title="${T_B}$ uncertainty due to uncertainties in ${O_2}$ and ${H_2 O}$ parameters",
            xlabel='Frequency [GHz]', ylabel='$\sigma_{T_B}$ [K]',
            label=[atmp.atm_profiles()[atmp.TROPICAL],
                   atmp.atm_profiles()[atmp.TROPICAL] + ' with ${H_2 O}$ ${n_{CS}}$ parameter'],
                   figsize=(12,8))
plt.grid()